scala Functor

Published: September 10, 2017 by

• Categories:
• scala-function 5

• Tags:
• functor 1
• scala 24
• 사상 1
• 스칼라 24
• 함자 2

scala Functor.

• 들어가기 앞서
• Functor
  • 잠깐! higher-kinded type(고계type) & existential type(존재 type)
• Functon law

들어가기 앞서

현장에서 프로젝트에 투입되면 spring 기반의 architecture로 일을 했다. 주로 batch 쪽을 담당했는데 업무팀의 요구사항에 연계되어 들어온 file format이 제각각이라 때에 따라서는 기존의 String batch Reader에 기능을 추가 구현하여 제공해주어야 할때가 더러 있다.

spring batch framework의 ItemReader 부분은 Template method 와 Strategy pattern으로 구성되어 있어 file format에 따라 data atrribute 부분를 쉽게 구성해서 기존 기능에 넣기만 하면 되는.. 참 spring-framework은 고마운 존재인 듯 하다.

물론 그것 뿐이겠냐만은 java의 design pattern을 이용하며 OOP 언어의 SOLID 법칙으로 설계 하는데 도움이 된다.

객체지향 언어도 그러하듯 함수형 언어도 함수의 일반적인 구조적 pattern 체계화 한다면 코드의 중복을 줄이고, 서로 다른 문맥이나 서로 다른 해법에서 공통 구조를 인식 할 수 있게 하지 않을까?

이러한 것에 도출되는 Functor와 Monad, Applicative Functor, Traversable Functor등이 필요한 이유일까 싶다.

Functor

functor를 이야기 하기 전에 아래의 예제 코드들을 보자.

scala> val a = 2
a: Int = 2
 
scala> val plusThree = (a:Int) => a + 3
plusThree: Int => Int = $$Lambda$1043/1967118241@12a2585b
 
scala> plusThree(2)
res0: Int = 5
 
scala> val xs = List(1,2,3,4,5)
xs: List[Int] = List(1,2,3,4,5)
 
scala> plusThree(xs)
:14: error: type mismatch;
 found   : List[Int]
 required: Int
       plusThree(xs)
                 ^

plusThree 는 Int => Int 으로 Int을 받아 3을 더하는 함수이다. 2을 넣으면 5가 결과로 나온다.
하지만 위에서 보는 것과 같이 List(1,2,3,4,5)은 error 가 발생한다.
그럼 List(1,2,3,4,5) 에 대한 3을 더하는 연산은 어떻게 해야 할까?
(List[Int] 와 같이 higher-kined type F[_] 를 앞으로 이야기 편하게 box라 부르기로 하자)

잠깐! higher-kinded type(고계type) & existential type(존재 type)

사실 위에 언급한 box라고 부르기로 한 것은 scala에서 지원하는 higher-kined type이다.
F[_] 이런 유형을 Higher-kinded type(고계타입)이라 한다. 이는 매개변수화한 타입 (여기서는 F)을 추상화 한 것 이다. 따라서 Higher-kinded type을 통해 매개변수화한 타입 자체를 추상화 할 수 있다. 이는 Functor, Monad, Applicative Functor, Traversable 등에 필히 등장 한다. 추후 람다 타입도 등장한다. 이는 추후에
반면 Seq[_] 은 existential type으로 Seq[T] forSome { type T }으로 Seq안의 매개변수 타입 추상화 한 것 이다.

다시 본론을 이어서

//xs map f 를 사용하지 않았다..
def fmap(xs: List[Int])(f: Int => Int): List[Int] = {
  def go(xs: List[Int], rs: List[Int]): List[Int] = xs match {
    case h::t => go(t, f(h) :: rs)
    case Nil => rs.reverse
  }
  go(xs,List.empty)
}

이제 List[Int]에 plusThree을 적용하자.

scala> val xs = List(1,2,3,4,5)
xs: List[Int] = List(1, 2, 3, 4, 5)
 
scala> fmap(xs)(plusThree)
res0: List[Int] = List(4, 5, 6, 7, 8)

위의 코드를 보면 fmap은 함수 f 를 List[Int]라는 box로 포장된 값에 적용한다.
이게 Functor다.
Functor는 함수를 box로 포장된 값에 적용하는 것이다.

이제 이를 typeclass로 표현 해보자.

trait Functor[F[_]] {
  def map[A,B](ma: F[A])(f: A => B): F[B]
}

위의 map 함수를 아래와 같이 위치를 수정해보면

def map(f: Int => Int)(xs: List[Int]): List[Int]
val plusThree = (a:Int) => a + 3
val functor = map(plusThree) _
functor: List[Int] => List[Int]

Int => Int 을 받아 List[Int] => List[Int] 로 function Int => Int 이 function List[Int] => List[Int]로 되었다. 이를 lift 승격 함수라 한다. 이는 아래의 그림과 같다.

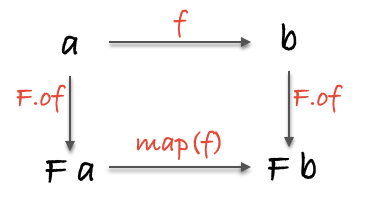
Functon law

1.Functor에 항등함수를 적용하면 원래의 Functor와 같다.
2.두함수가 있을때 두함수의 합성을 한후 Functor에 적용한 것은 Functor에 한 함수를 적용하고 난 후의 Functor에 나머지 함수를 적용한 것과 같다.
3.구조를 보존해야 한다.

1의 법칙을 코드로 표현하면 아래와 같다.

//항등 함수 
def id[A] = (a:Int) => a
map(ma)(id) == ma

2의 법칙을 코드로 나타내면 아래와 같다.

f1: A => B
f2: B => C
map(ma)(f2 compose f1) == map(map(ma)(f1))(f2)

3의 법칙은 map(List[A])(f) 의 결과는 List[A]의 구조를 변경해서는 안된다. 이는 List[A]의 길이가 같고, 해당 요소들은 같은 순서대어야 한다. 예를 들어 예외를 던지거나, 요소를 제거하는 등은 안 된다.
거울에 비친 자신의 모습을 볼때, 거울에 보이는 모습은 나를 project하여 비추어진 결과이다.
이는 나의 형태에 모습(구조)을 그대로 반영 한다. 이는 Functor의 조건과 같다.
Functor만으로는 할 수 있는 것이 제한적이다. Functor는 추후 설명할 Monad의 flatMap, Applicative Functor 의 map2등에 사용된다.

Functor는 여기까지 하고 다음에는 Monad에 대해서 글을 올리겠다.